A perfect matching of a graph is a matching (i.e., an independent edge set) in which every vertex of the graph is incident to exactly one edge of the matching. A perfect matching is therefore a matching containing $n/2$ edges (the largest possible), meaning perfect matchings are only possible on graphs with an even number of vertices.
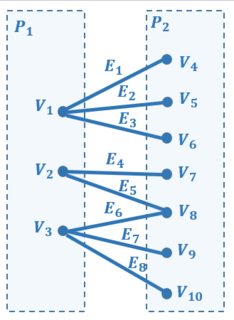
However below graph contains even number of vertices (10 vertices), but still I cant guess the perfect matching – in which every vertex of of the graph is incident to exactly one edge. One of the matching can be ${E_1,E_4,E_6}$. However not every vertex (here, ${V_5,V_6,V_9,V_{10}}$) is incident to exactly one edge in this matching as required by above definition. So this is not definitely a perfect matching as desired by wolfram’s definition. Also I cannot add any other edge to this matching as it will make two edges to share a vertex. Q1. Is perfect matching possible with this graph?  I am also reading the same topic from the book by Narsingh Deo. It defines the complete matching in the context of bipartite graph:
I am also reading the same topic from the book by Narsingh Deo. It defines the complete matching in the context of bipartite graph:
In a bipartite graph having a vertex partition $V_1$ and $V_2$ a complete matching of vertices in set $V_1$ into those in $V_2$ is a matching in which there is one edge incident with every vertex in $V_1$. In other words, every vertex in $V_1$ is matched against some vertex in $V_2$.
I am not able to understand if these two (wolfram’s and book’s) definitions point to two different concepts or they are one and same. By my understanding, according to Deo’s definition, $V_2$ may contain more vertices than that in $V_1$, thus the size matching may be less than $n/2$. However, wolfram says perfect matching contains $n/2$ edges. For example in above graph the complete matching of vertices in set $P_1$ into those in $P_2$ can be ${E_1,E_4,E_6}$ as one edge in this matching is incident with every vertex in $P_1$. Q2. So the two definitions (wolfram’s and book’s) must be different concepts. Am I correct?
Asked By : Mahesha999
Answered By : Yuval Filmus
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/50410