
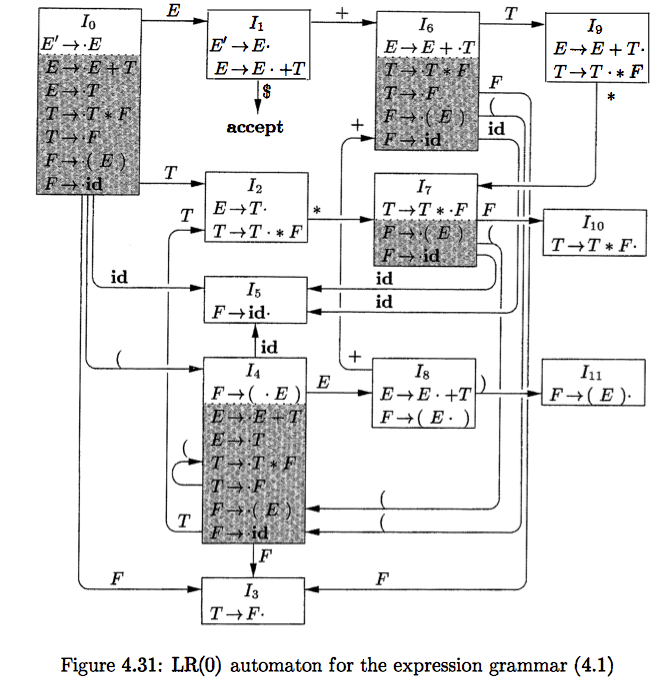
 In addition, is closure of item sets related to with calculating them? If so, what exactly every item in I1, I2, … , and I11 is?
In addition, is closure of item sets related to with calculating them? If so, what exactly every item in I1, I2, … , and I11 is? 
Asked By : inherithandle
Answered By : Tim
T -> T * . F
Step 2 of CLOSURE is saying that since F is in front of the dot we have to expand it, adding those items to the itemset. Hence, we add items the following items.
F -> . ( E ) F -> . id
This is everything that F can expand to. So the full itemset is now:
T -> T * . F F -> . ( E ) F -> . id
We reapply rule (2), but see that the . is not in front of any new non-terminals that we haven’t expanded, we are done. The itemset is now closed. The other half of the parse table building algorithm generates new itemsets. This involves moving the dot across each symbol of each item. For example, moving the over the ‘F’ gives you the itemset with the kernel item below.
T- > T * F .
This is I10 in your diagram. Note, that edges from I7 to I10 is labeled F (since the dot crossed that symbol). You’d reapply the same closure algorithm here and loop this process. See the Wikipedia entry on this for more information.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/25924 Ask a Question Download Related Notes/Documents