Problem Detail: While going through certain problems. it seems that more than one NFA is possible for the given language. Is it so? For example for drawing: NFA ending with 1 where $Sigma={0,1}$ is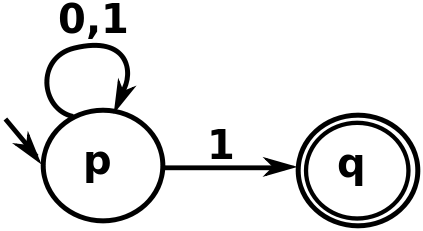 
and also we can draw one without 0 from the edge P to P! Which one should be considered “more” correct?
and also we can draw one without 0 from the edge P to P! Which one should be considered “more” correct?
Asked By : user5507
Answered By : vonbrand
There are many, many different NFAs accepting a particular language, or DFAs for that matter. You can just add branches that lead into dead ends at will, for example. Or add detours that give the same result as the main road, like in your automaton adding a new state $r$, with transitions from $p$ to $r$ on 1, and then from $r$ to $r$ on 0 and 1, and finally from $r$ to $q$ on 1. In the given case, omitting the transition from $p$ to $p$ on 0 gives another language. You should convince yourself that the modified NFA doesn’t accept anything containing zeros.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/21515 Ask a Question Download Related Notes/Documents
